푸리에급수 : 주기함수 -> 삼각함수의 급수로 표현
모든 주기함수 -> 진폭, 주파수가 다른 정현파들의 급수로 표현
예시 : \[x(t)=sin(2\pi*1t)+1/3sin(2\pi*3t)+1/5sin(2\pi*5t)\]
연속시간 푸리에급수(CTFS) : 연속시간 주기신호들의 합성
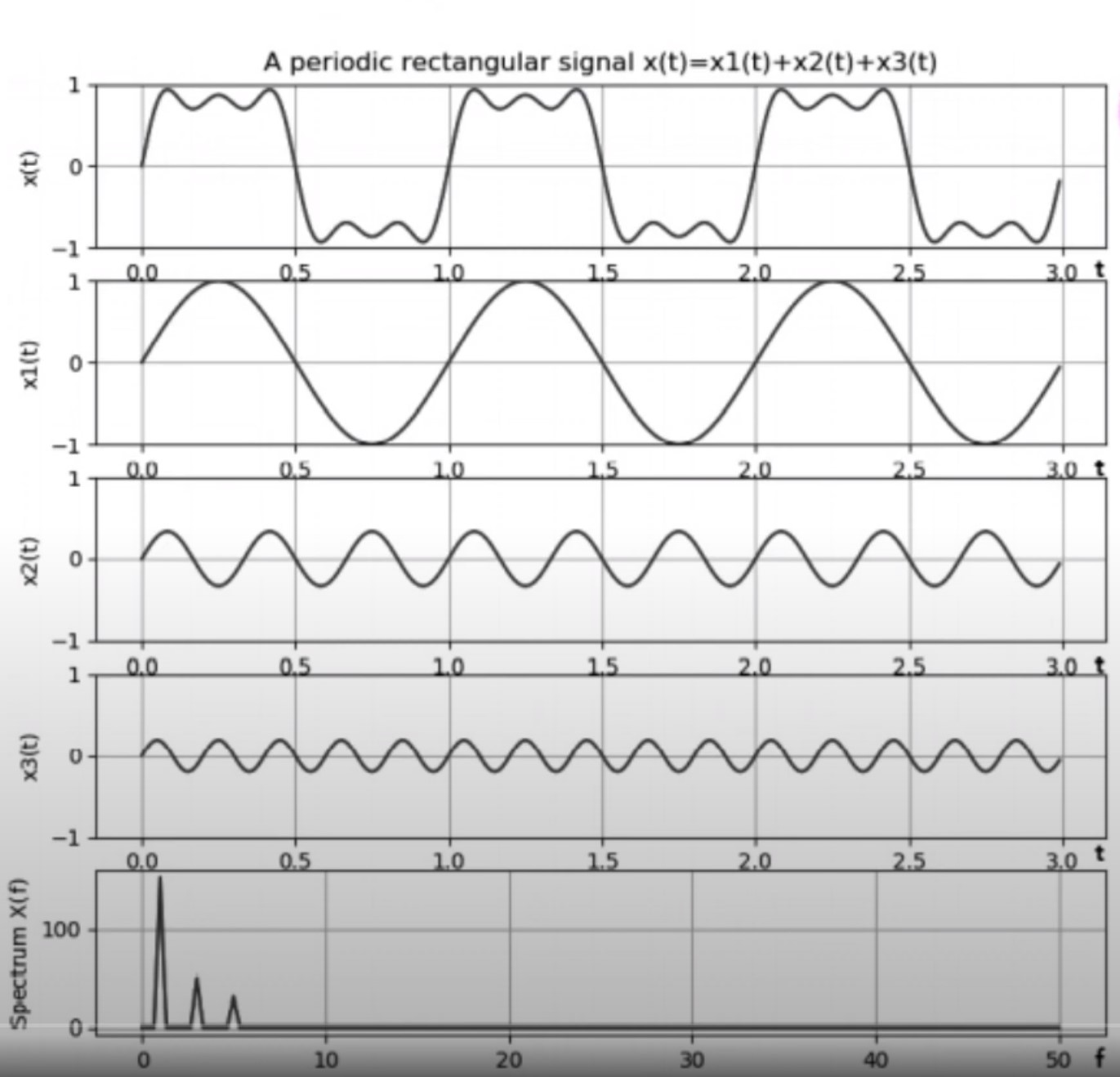
위의 표에서 x1(t)와 x2(t), 그리고 x3(t)을 모두 더한 그래프는 맨 위에있는 그래프이며, 마지막 그래프는 각 주파수에 대한 값들을 그래프로 그린 내용이다.
즉 연속시간 주기신호들을 합성하여 특정한 신호를 그래프로 그릴 수 있으며 이 그래프를 푸리에 급수를 통해 확인하게 되면 각 주파수마다의 Mgnitude와 주파수를 확인할 수 있다.
삼각함수에 의한 연속시간 푸리에급수
연속시간 주기신호의 푸리에급수 -> 삼각함수식으로 일반화 가능
\[x=a_0+\sum_{k=1}^{}a_kcos(kw_0t)+\sum_{k=1}b_ksin(kw_0t)\]
\[a_k=2/T\int_{T}^{}x(t)cos(kw_0t)dt \]
\[b_k=2/T\int_{T}^{}x(t)sin(kw_0t)dt \]
\[w_0=2\pi f_0\]
기저신호 : 푸리에 급수를 구성하는 각 항의 신호, 기저신호 이용한 정현파신호는 기본주파수 f의 정수배인 고조파신호
--> 고조파신호끼리 직교하는 성질
복소지수에 의한 연속시간 푸리에급수
오일러공식을 이용하여 정현파 신호에 대입해보자.
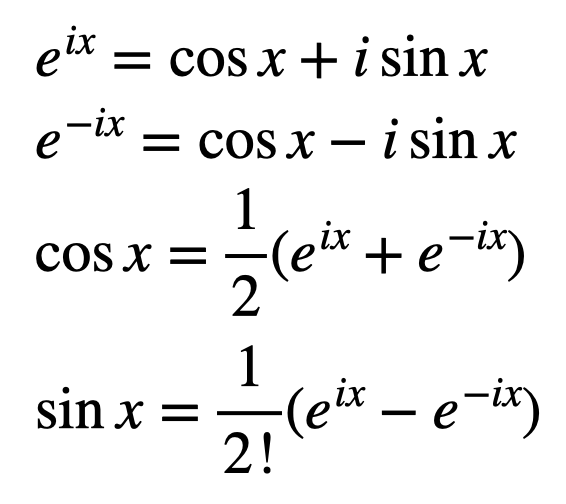
\[\sum_{k=1}^{}a_kcos(kw_ot)+\sum_{k=1}^{}b_ksin(kw_ot)=\sum c_ke^{jkw_0t}+\sum c_ke^{-jkw_0t}\]
\[x(t)=\sum c_ke^{jkw_0t}\]
\[c_k=1/t\int_{T}^{}x(t)e^{-jkw_0t}dt=1/T\int_{T}x(t)e^{-j2\pi f_0t}dt\]
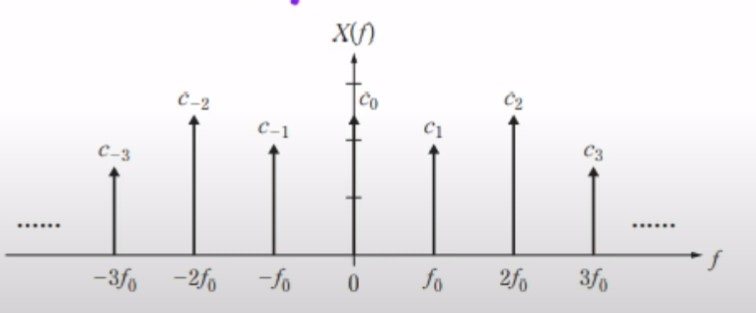
즉 C의 값과 x에 값은 정현파 신호를 통해 오일러 공식에 대입하여 복소지수로서 표현이 가능하다.
또한 이 값들은 주기 f0을 일정한 간격으로 가지고 있는 선스펙트럼 형식으로 표현이 가능하다.
'신호처리' 카테고리의 다른 글
| [Signal Processing] 샘플링과 복원(Sampling, reconstruction) (2) | 2023.10.04 |
|---|---|
| [Signal Processing] 연속시간 푸리에변환 (0) | 2023.10.04 |
| [Signal Processing] 연속시간신호의 분석(정현파 신호와 복소지수 신호) (0) | 2023.09.22 |
| [Signal Processing] 디지털 신호처리 개요(신호란 무엇인가) (0) | 2023.09.21 |



