샘플링
x(t)는 적분가능한 연속시간신호일 때
CTFT(연속시간 푸리에변환)
\[X(\omega)=\int x(t)e^{-jwt}dt\]
ICTFT(연속시간 푸리에 변환)
\[x(t)=1/2\pi\int X(\omega)e^{jwt}d\Omega \]
연속시간 푸리에변환인 X(w)를 크기조정(scale) 및 주파수 조정(frequncy) 마지막으로 이동함으로써 아날로그 라디안주파수인 (w)를 디지털 라디안주파수로 변환하게 된다.
\[x(\Omega)=1/T_s\sum x(w/T_s-2\pi l/T_s)\]
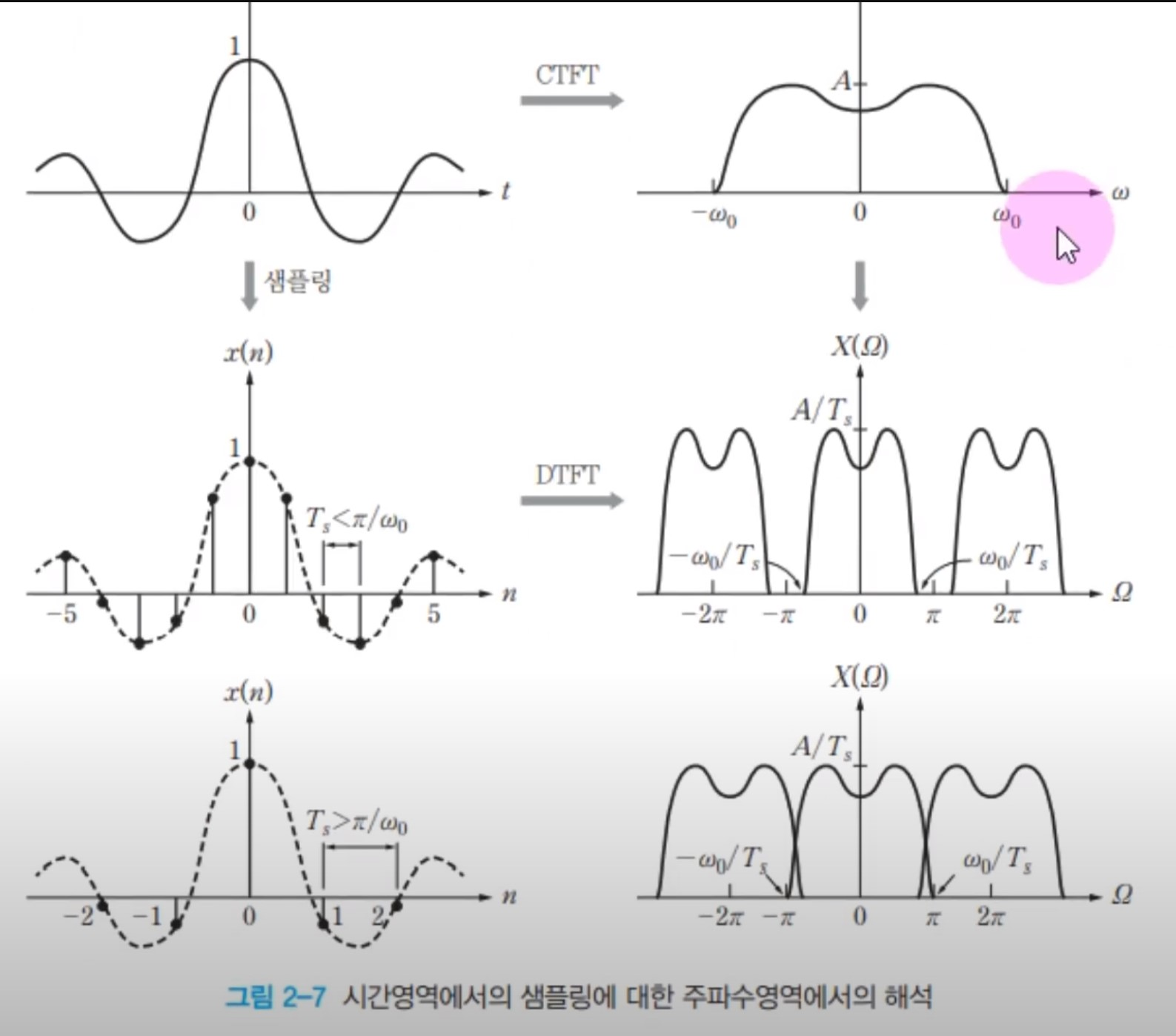
샘플링 정리
대역폭 w0를 한정하였을 때, x(t)는 fs가 x(t)의 대역폭 w0보다 두배보다 크면 복윈이 가능하다.
x(t) 샘플링 후 얻은 이산시간신호 x(n)의 가장 높은 아날로그주파수는 f/2[Hz]이다.
복 원
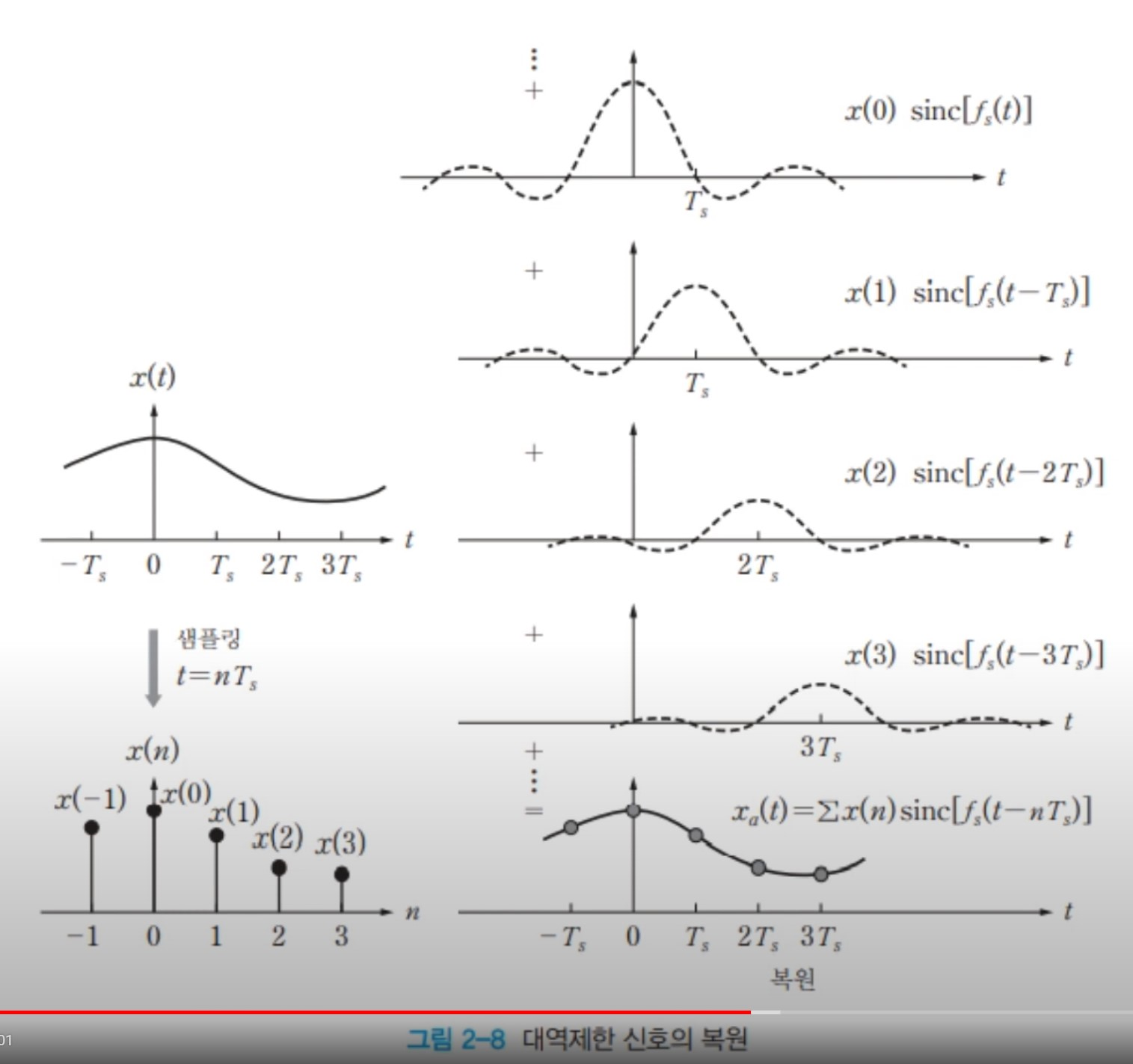
1. 샘플들을 가중치 임펄스 열로 변환한다.
\[\sum x(n)\delta(t-nT_s)=...+x(-1)\delta(t+Ts)+x(0)\delta(t)+x(2)\delta(t-T_s)+...\]
2.[-f/2, f/2] 구간으로 대역이 제한된 이상적인 아날로그 지역통과필터(sinc함수)로 필터링한다.
\[x_a(t)=\sum x(n)sinc[f_s(t-nT_s)]\]
\[\therefore sinc(x)=sin(\pi x)/\pi x\]
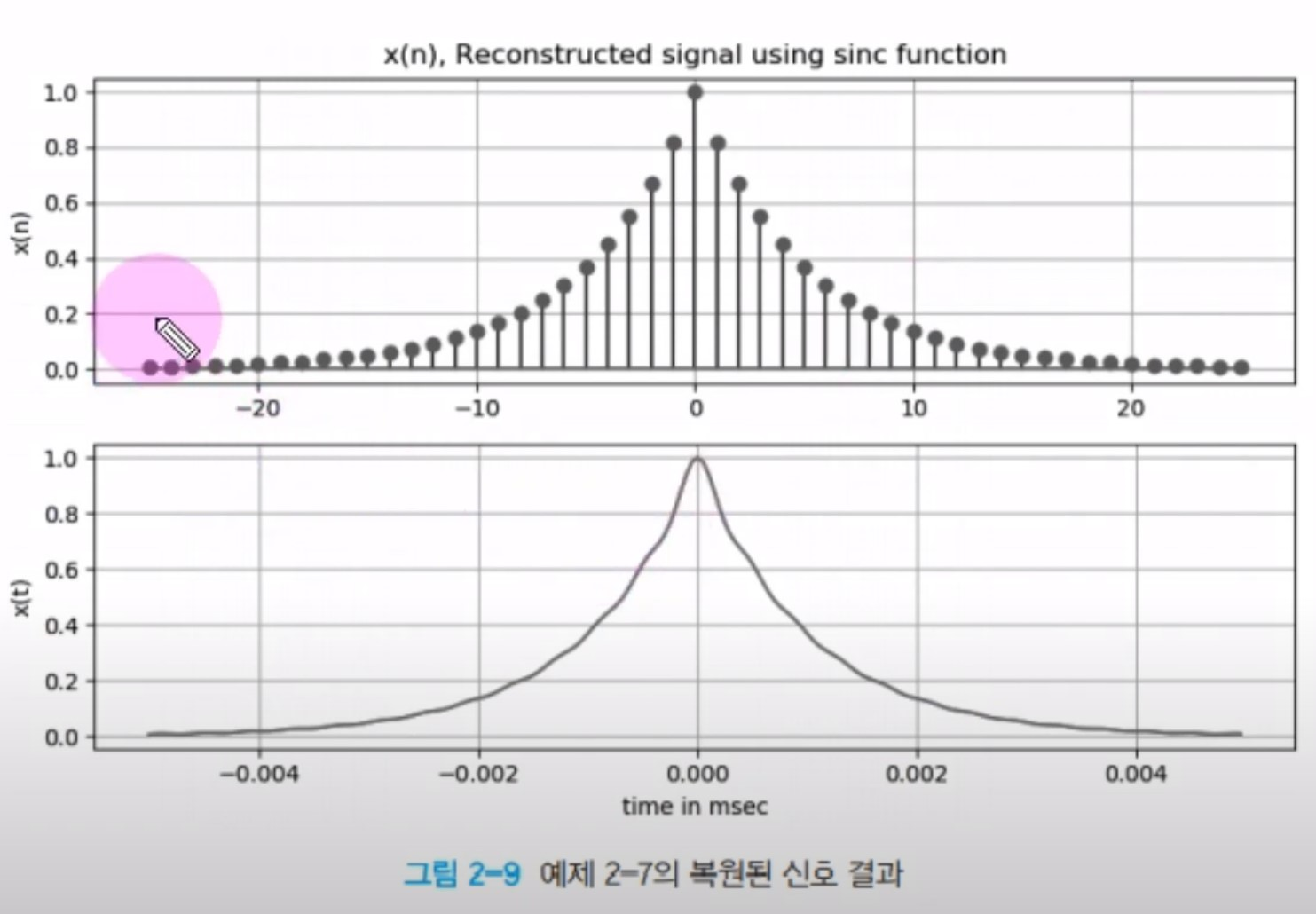
실질적인 D/A 변환기
1. 영차유지보간 : 현재~다음 샘플까지 구간 동안을 현재 샘플값으로 일정 유지한다.
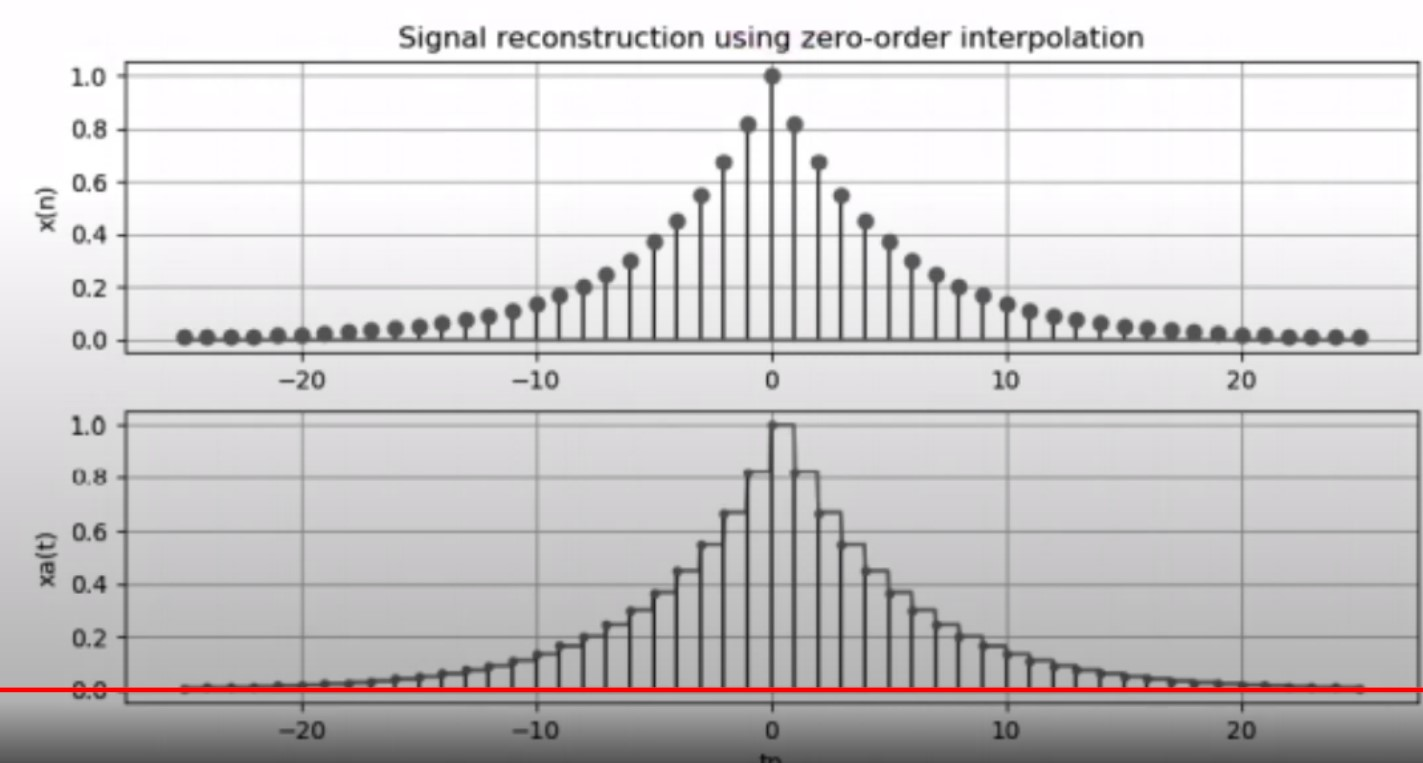
2. 일차유지 보간 : 이웃 샘플 사이 직선적으로 연결하는 방법
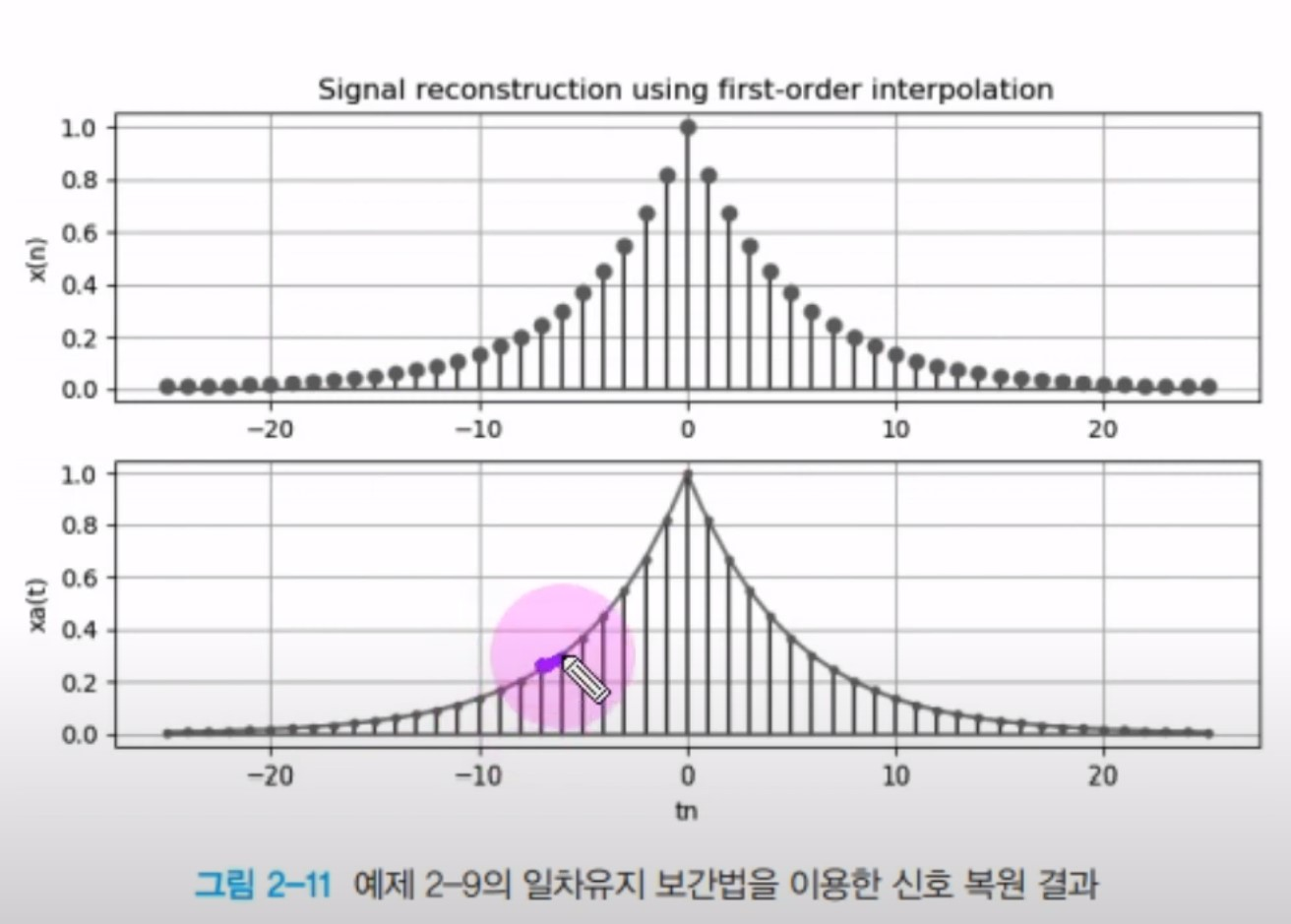
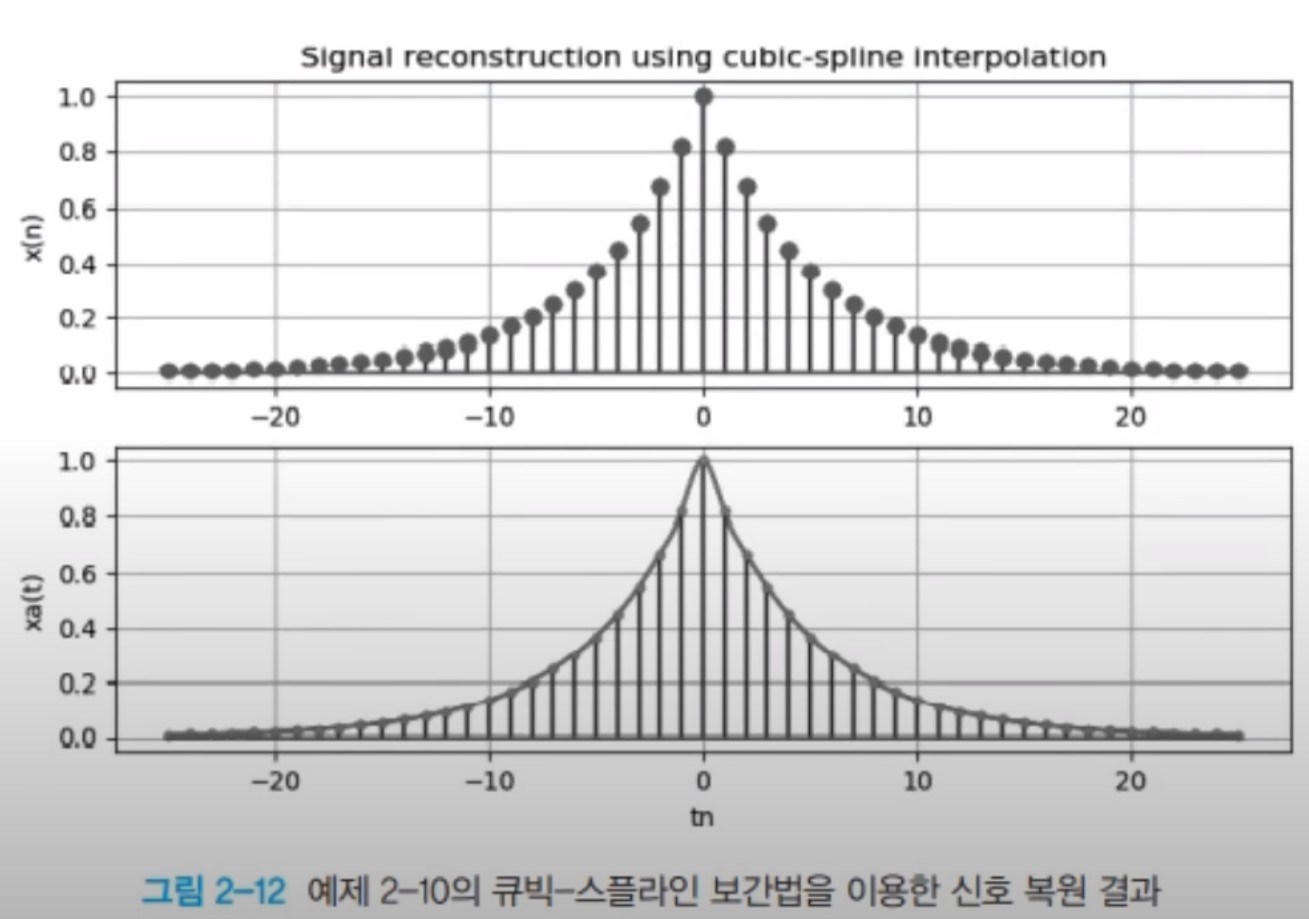
3. 큐빅-스플라인 보간 : 3차 보간식 적용
'신호처리' 카테고리의 다른 글
| [Signal Processing] 연속시간 푸리에변환 (0) | 2023.10.04 |
|---|---|
| [Signal Processing] 연속시간 푸리에급수 (0) | 2023.10.04 |
| [Signal Processing] 연속시간신호의 분석(정현파 신호와 복소지수 신호) (0) | 2023.09.22 |
| [Signal Processing] 디지털 신호처리 개요(신호란 무엇인가) (0) | 2023.09.21 |



